Linear Algebra is a mathematical tool which is a study of vectors and matrices. It is very important to understand the intuition behind how a Machine Learning algorithm works. Linear Algebra will help us understand the algorithm theoretically so that we know when to apply a particular algorithm based on the problem given. To be a good Machine learning engineer/a Data Scientist one has to master some of the important concepts of Linear Algebra. We use vectors and matrices to represent the data, also vectors and matrices can be represented as Linear Equations.
Vectors and Matrices:
A scalar is a single number. For example: [3] or [10].
A vector is an ordered list/array of numbers that can be arranged either as a row or a column. Order is very important in a vector. Consider the below image having two vectors V1 and V2. The vector V1 is called a Row Vector since the vector is having only one row. Similarly, the vector V2 is called a Column Vector since it is having only one column. By default, we assume a vector as a column vector.
V1 = [ 1 4 7], V2 = ![]()
Matrix is an arrangement of numbers in a rectangular array comprising of rows and columns. The order of the matrix is denoted by m x n, where m is the number of rows and n is the number of columns. Consider the below examples. A is a matrix of order 3 x 3 and B is a matrix of order 3 x 2.
A= , B =

![]()
A Tensor is a matrix in high dimensional space. It consists of depth along with rows and columns. The below example will explain a tensor and its order.
Point:
What is a Point? A point is represented as a vector. Consider the figure (a) below where x and y are the axes. Point A (2,3) is marked. This can be represented as A = [ 2 3] in vector form where 2 is called x component and 3 is called y component. The point A is represented in 2-D space. Similarly, the point B = [1 2 6 8 4 7 . . . n] is an n-dimensional point represented in nD space.
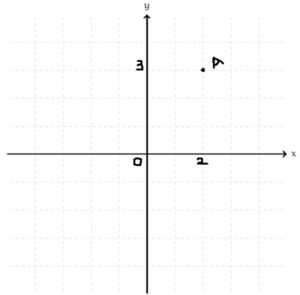
(a) Plot showing a point marked A (2,3)
Basic Operations on vectors:
Let us see some basic operations on vectors which are used ML. Let X = [ x1 x2 x3 x4 …… xn], Y = [ y1 y2 y3 y4 …… yn].
1. Addition of two vectors: It is nothing but component-wise addition and resultant is also a vector.
X + Y = [ x1+y1 x2+y2 x3+y3 ……… xn+yn]
2. Distance between two vectors/two points:
Let X= [x1 x2], Y= [y1 y2]. It is given by the below formula. D = √[ (x1-y1)2 + (x2-y2)2]. The distance of two nD points is given by:
D = √[ (x1-y1)2 + (x2-y2)2 + (x3-y3)2 …… (xn-yn)2]
3. Product of two vectors: There are two types of product namely Dot product and Cross product in vectors. We use dot products extensively in Machine Learning. It is also component-wise multiplication followed by addition. The result is a scalar.
X.Y = x1y1 + x2y2 + x3y3 + …. +xnyn
We will see the matrix form of expressing the product of two vectors in a while.
Basic operations on Matrices:
Addition and Multiplication of matrices are the important Linear Algebra concepts for ML.
- Addition of Matrices: This is also component-wise addition as seen in vectors. Refer to the below image for an example.
- Multiplication of two matrices: We have three types as given below.
- Scalar Multiplication: It is component-wise Multiplication with a scalar. Let k = 2 is a scalar multiplied with a Matrix A, then
![]()
- Vector Multiplication: It is component-wise multiplication followed by addition. Let A = , B = A is of order 1 x 2. B is of order 2 x 2. The resultant is 1 x 2.
A x B = [ (1×1 + 2×1) (1×0 +2×2)] = [ 3 4]
- Matrix-Matrix Multiplication: This is also component-wise multiplication followed by addition.
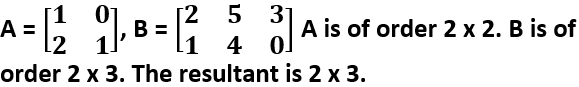
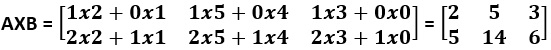
- Transpose of a Matrix: The transpose of Matrix A is denoted as AT. It is nothing but interchanging of rows and columns of a matrix A. For example:

Matrix form of expressing the product of two vectors: This is very important in understanding the Logistic regression algorithm and basic concepts of Neural Networks. Product of two vectors is given as:
-
- Y = x1y1 + x2y2 + x3y3 + …. +xnyn
can be rewritten as
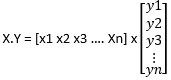
in Matrix form which gives the same result as X dot Y. So, X.Y = XT Y.
Note: Both X and Y are assumed to be column vectors.
Linear Equations:
Matrices and vectors can be represented in the form of Linear equations. Let us with the basic equation of a line. The general form of equation of a line is
ax + by + c = 0 —— (a)
We know, from (a) we get an equation of line as y = mx + b. Where m = -a /b which is slope, b = -c/b which is an intercept term. Let us stick on to general form which is (a). It can be re-written by changing notations as follows: ax+ by + c = 0 ->1
ax1 + bx2 + c = 0 ->2
w1x1 + w2x2 +w0 = 0 ->3
w0 + w1x1 + w2x2 = 0 ->4
![]() Vector form
Vector form
w0 + WT X = 0 ->6 Final Equation in matrix form
From above, Equation 5 is the vector form. By default, each vector is represented as a column vector. X is a column vector of order 2 x 1 and W is also a column vector of order 2 x 1. Transpose of W will give us a row vector of order 1 x 2. So, by matrix multiplication, we get the result as w1x1 + w2x2. This is how we arrived in equation 6. Equation 6 is a very important notation and one has to understand this at any cost. The term W is called Weight in ML terminology.
The figure we get in 2D space is a Line. A line in 2D is called a Plane in 3D. In higher dimensions, it is called a Hyperplane(nD). If the equation of a line is passing through the origin, then the intercept term w0 = 0. The Final equation is written as WT X = 0.
Some of the concepts where Linear Algebra is used in ML:
- Logistic Regression
- Neural Networks
- Principal Component Analysis (PCA)
- Single Value Decomposition (SVD)
- Deep learning algorithms like CNN’s uses a Tensor concept
- Preprocessing algorithms like One hot Encoding
